Bezpłatny fragment - Geometria rozszerzona

Kwadrat

Wstęp

Kwadrat to czworoboczna figura, która powstaje przez połączenie 4 segmentów linii. Segmenty linii w kwadracie mają wszystkie równe długości i łączą się, tworząc 4 kąty proste.

Obwód

Obwód kwadratu o boku A liczymy jako A*4

Przykład

Kwadrat o boku A=5cm

Obwód liczymy 5cm*4=20cm

Odpowiedź

Obwód kwadratu wynosi 20cm

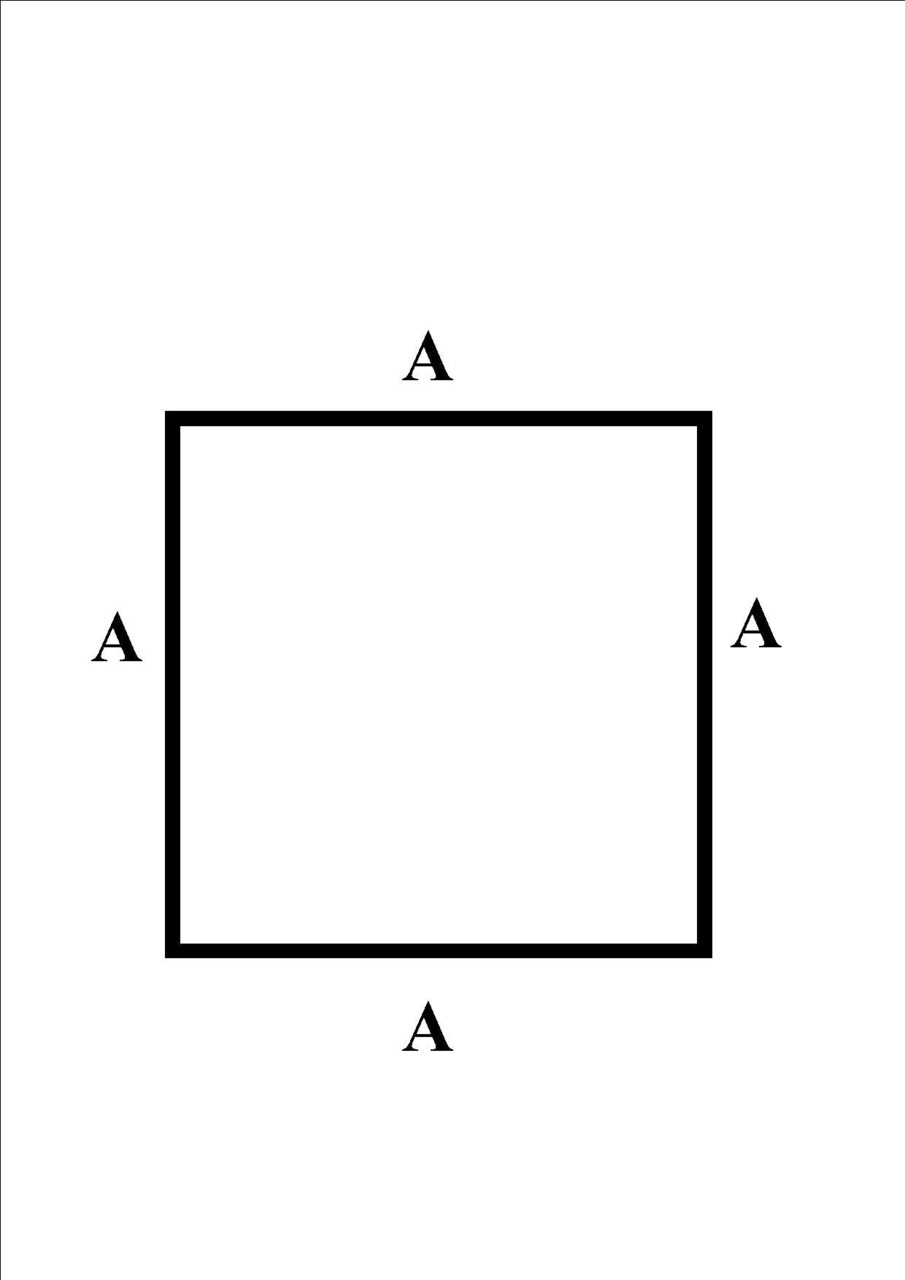
Pole

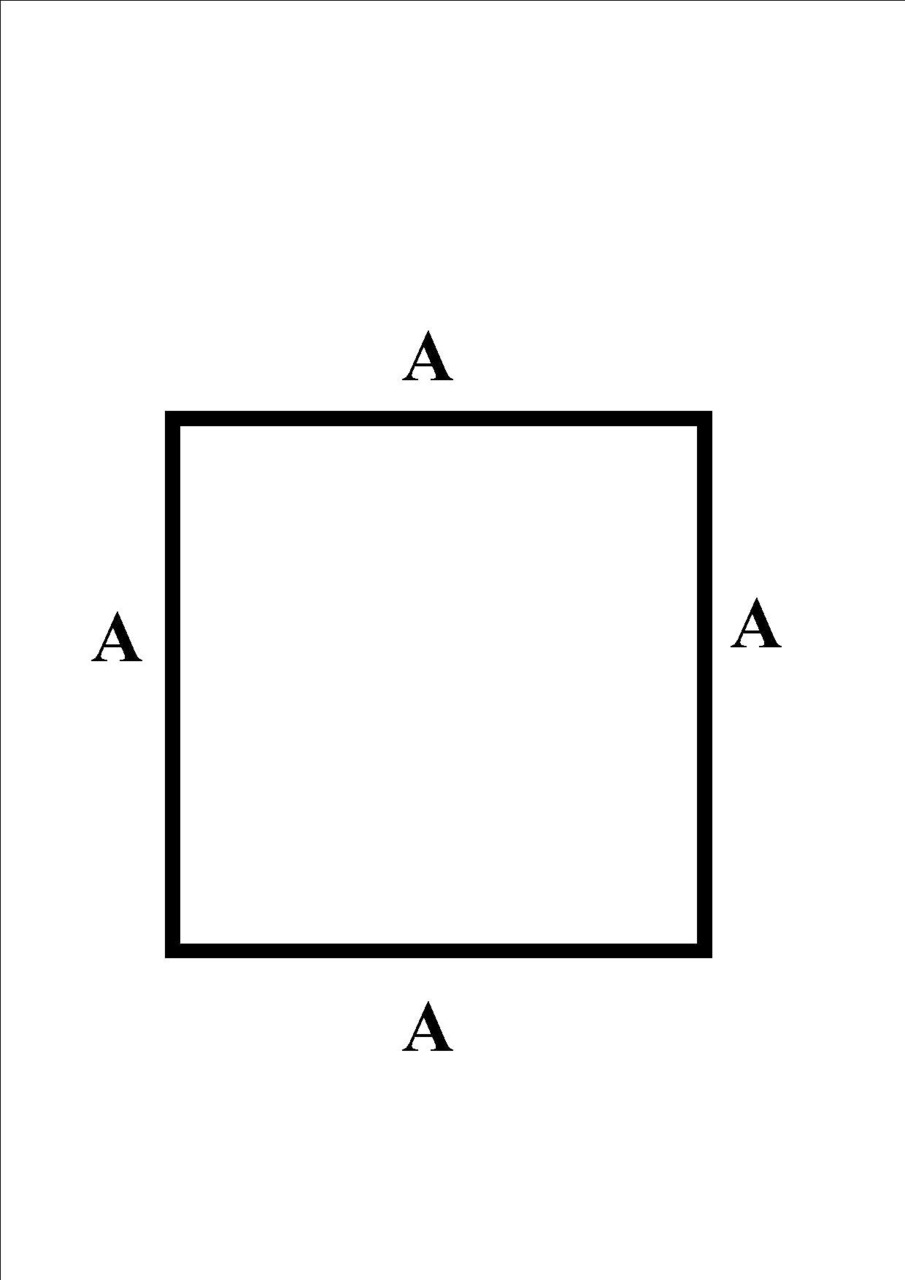
Pole kwadratu o boku A liczymy jako A*A

Przykład

Kwadrat o boku A=5cm

Pole liczymy 5cm*5cm=25cm2

Odpowiedź

Pole kwadratu wynosi 25cm2

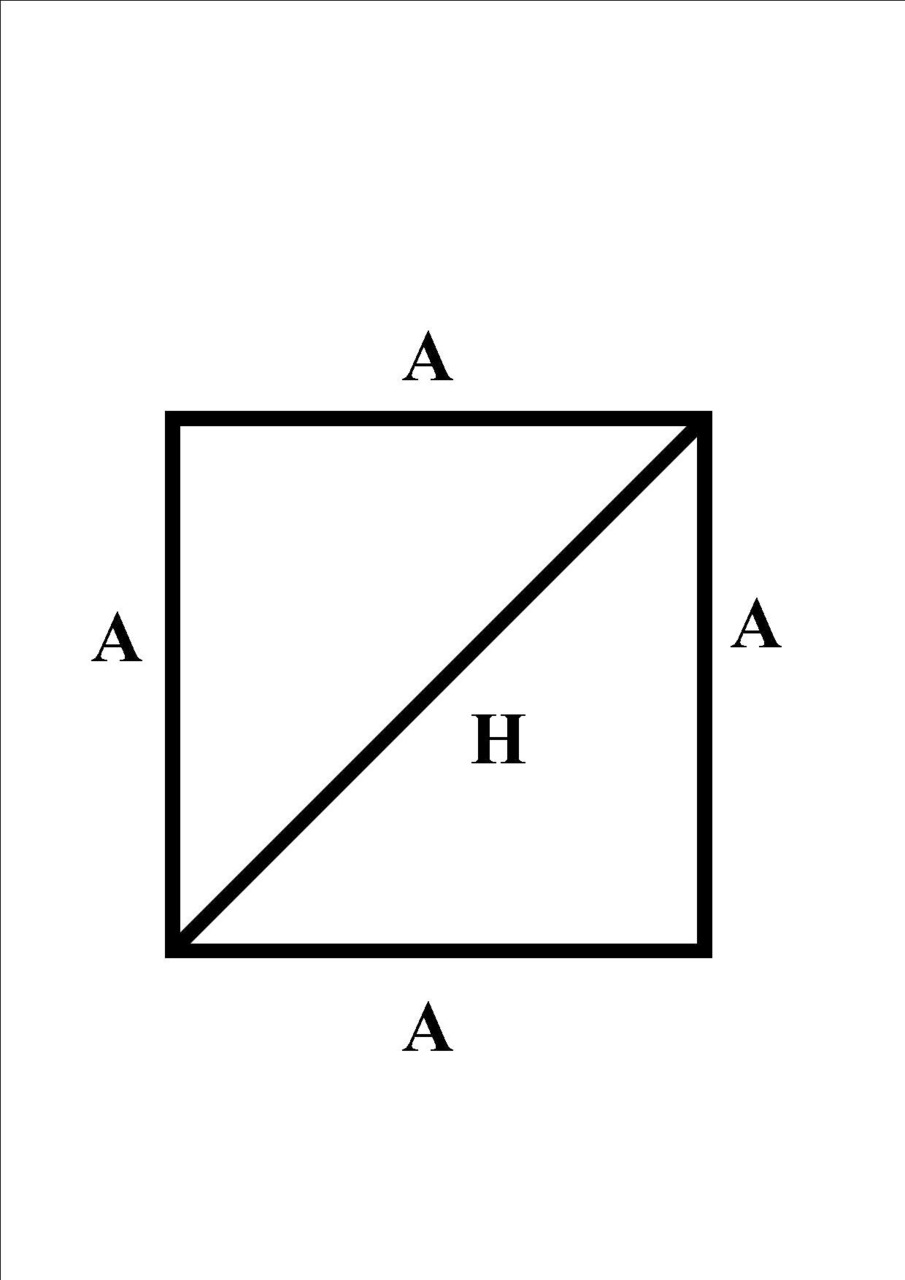
Przekątna

Przekątną kwadratu o boku A i przekątnej H liczymy.

1 Sposób. H= A*√2,

2 Sposób. A² + A²= H²

Sposób 2 odnosi się do twierdzenia Pitagorasa, który głosi, że: Jeżeli trójkąt jest prostokątny to suma kwadratów długości dwóch krótszych boków trójkąta jest równa kwadratowi długości najdłuższego boku.

Przykład

Kwadrat o boku A=5cm

Przekątną liczymy

1 Sposób. H²= 5*√2cm

2 Sposób. 5²+5²= H²

25+25 = H²

50 = H²

H= √50= 5√2cm

Odpowiedź

Przekątna kwadratu jest równa 5√2cm

Koło i Okrąg

Koło

Koło — jest zbiorem wszystkich punktów na płaszczyźnie, których odległość jest mniejsza, lub równa pewnej odległości (promień koła) od ustalonego punktu (środek koła).

Okrąg

Okrąg — jest zbiorem wszystkich punktów na płaszczyźnie, których odległość jest równa pewnej odległości (promień koła) od ustalonego punktu (środek koła).

Różnica miedzy kołem i okręgiem

Koło od Okręgu różni się tym, że okrąg jest „pusty w środku” zawiera tylko promień, obwód, a nie posiada pola. Koło zawiera obręcz oraz wszystko co w nim się znajduje, czyli Koło posiada obwód oraz pole.

Obwód

Obwód koła to krzywa biegnąca wzdłuż krawędzi okręgu. Obwód koła nazywany jest również obwodem koła. Obwód okręgu jest oznaczony literą C. Jest nieco większy niż trzykrotność jego średnicy. Jest to π średnicy koła. Obwód jest mierzony w cm, m lub km.

Obwód koła liczymy w następujący sposób:

Wzór na obwód koła

O = 2 * π * r

O — obwód koła

π — liczba pi = 3,1415

r — promień koła

Przykład

Obwód koła o promieniu 2cm liczymy następująco:

r= 2cm

O = 2 * π * 2cm

O= 2*3,1415*2cm=12,566cm=12,57cm

Odpowiedź

Obwód koła wynosi 12,57cm

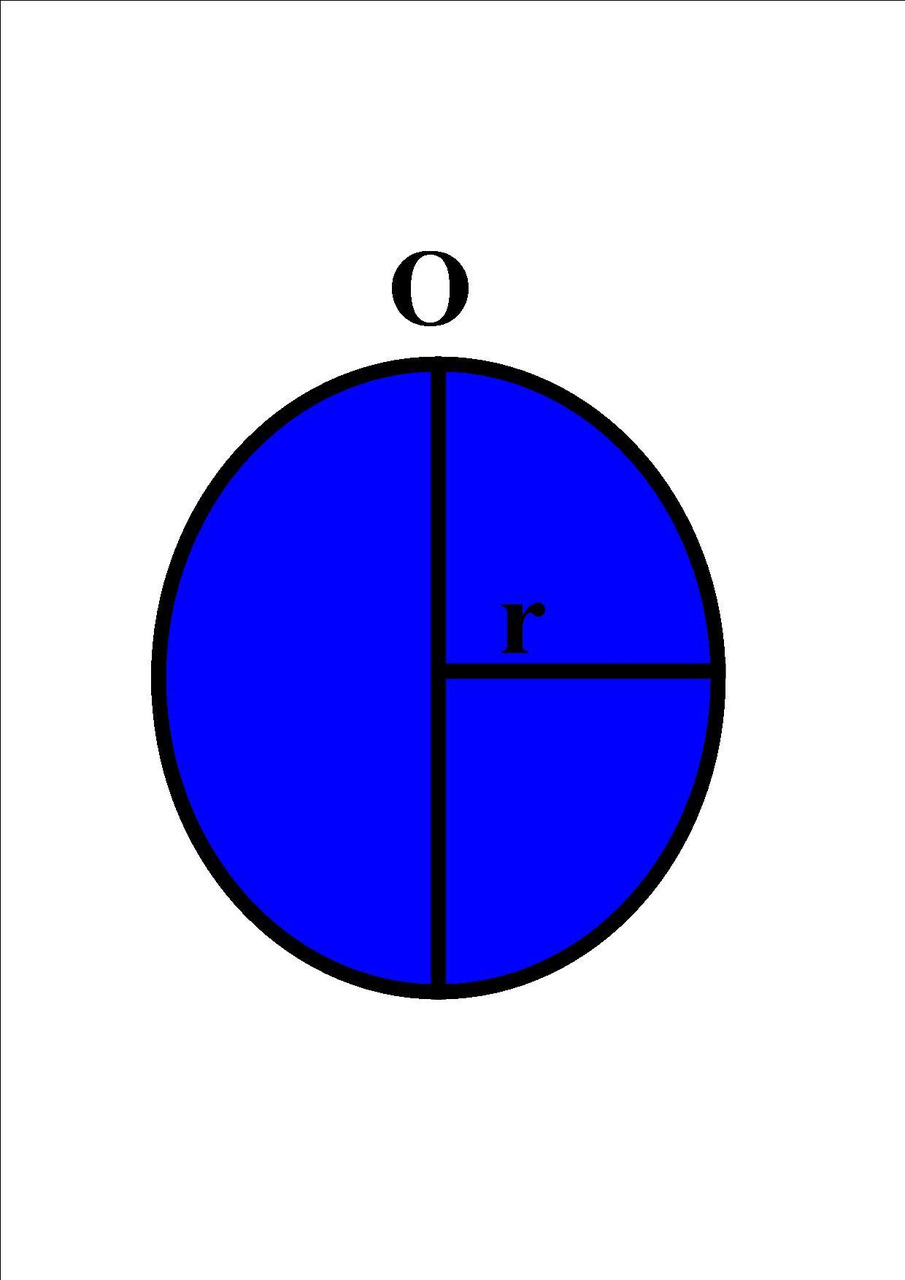
Pole koła

Wzór na pole koła

P= π* r²

P — pole koła

π — liczba pi = 3,1415

r — promień koła

Przykład

Pole koła o promieniu 2cm liczymy następująco:

r= 2cm

P= π*2²

P= 3,1415*2²= 3,1415*4=12,566=12,57cm²

Odpowiedź

Pole koła wynosi 12,57cm²

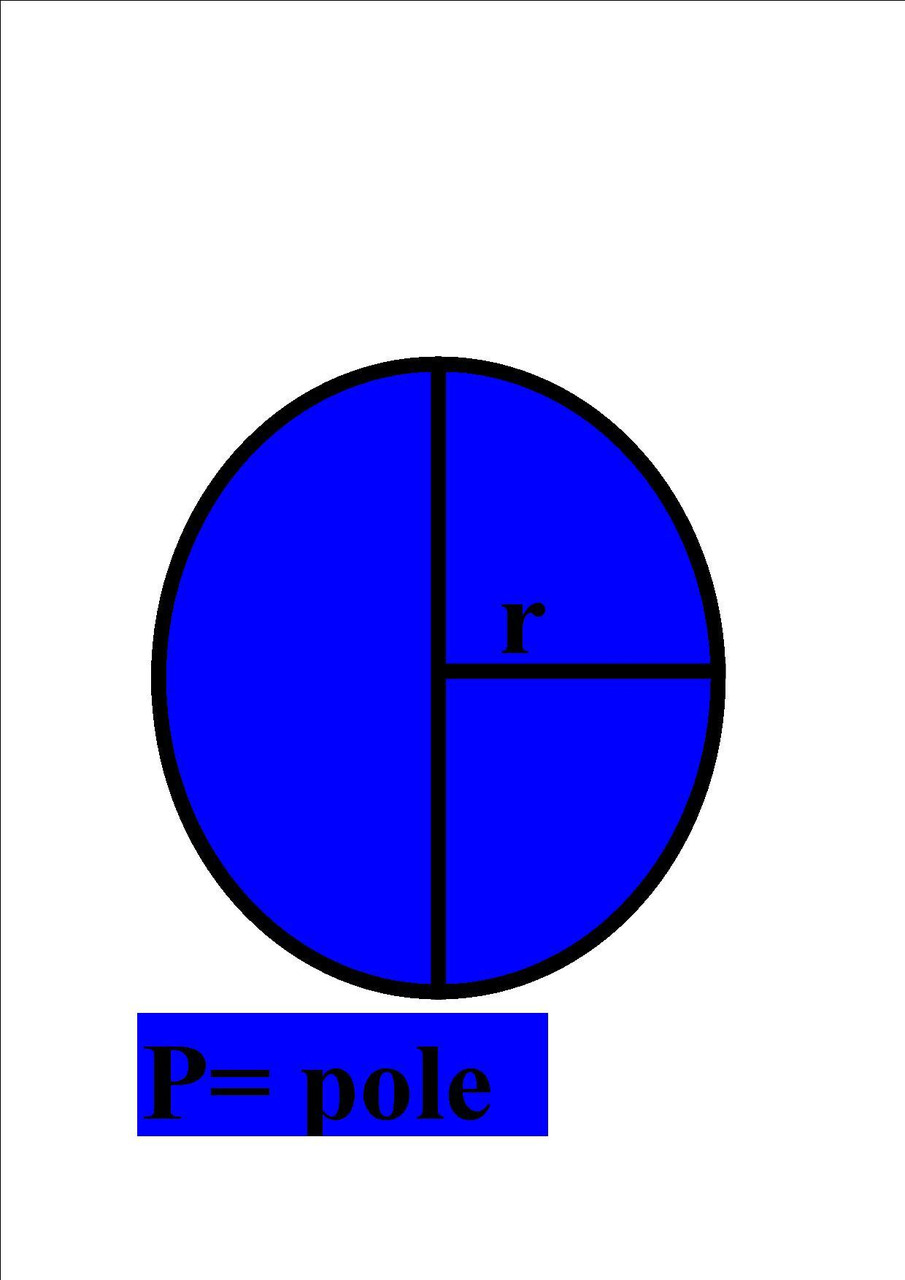
Promień koła

Aby obliczyć promień koła znając jego obwód należy przekształcić wzór na obwód koła, który wygląda następująco.

Wzór na obwód koła

O = 2 * π * r

O — obwód koła

π — liczba pi = 3,1415

r — promień koła

Po przekształceniu wzór na promień koła wygląda następująco.

O = 2 * π * r

r= O/2π

Przykład

Obwód koła wynosi 12,57cm ile wynosi promień?

Rozwiązanie.

O=12,57cm

r= 12,57/2π

r= 12,57/2*3,1415

r= 12,57/6,283

r= 2cm

Odpowiedź

Promień koła wynosi 2 cm.

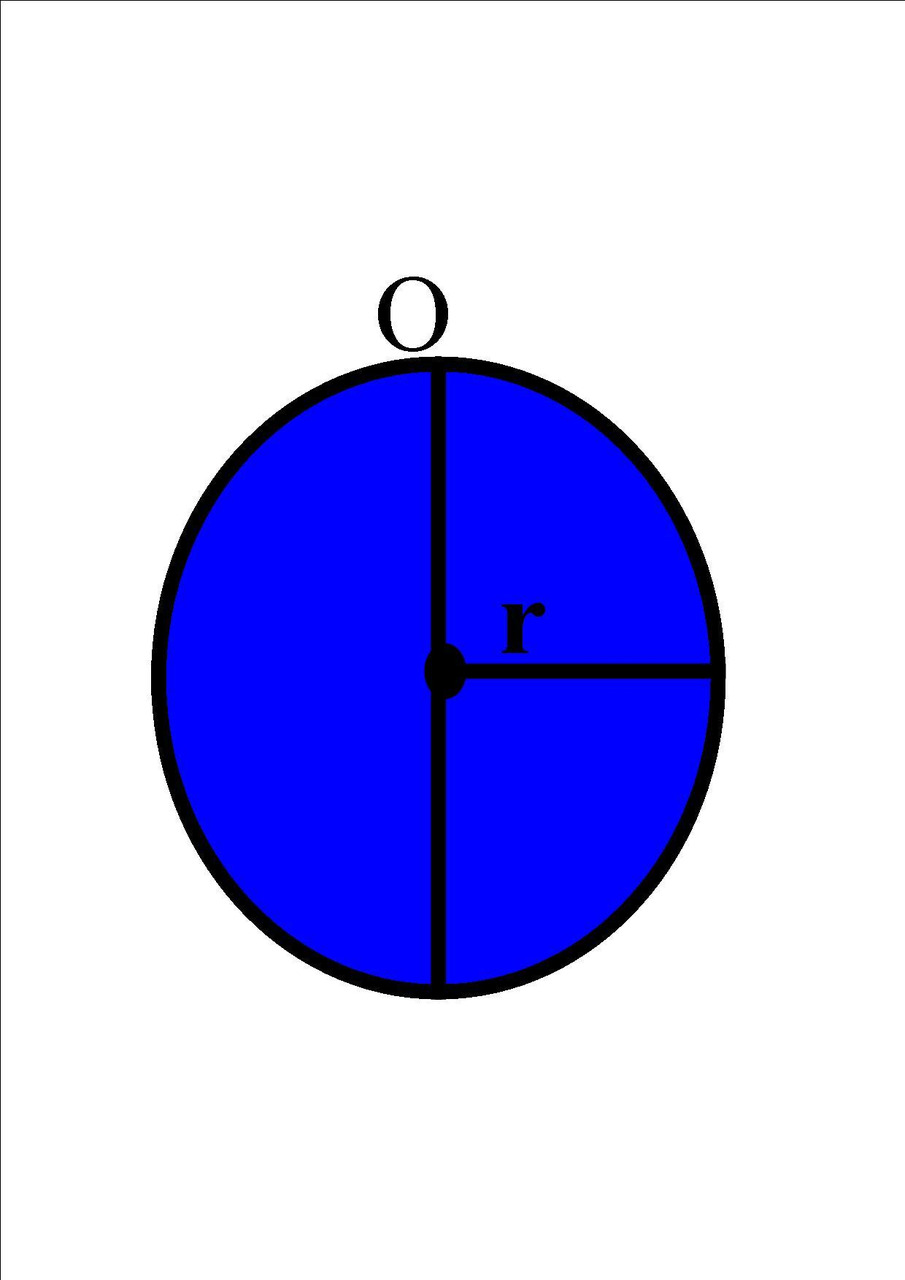
Trójkąt

Wstęp

Trójkąt składa się z trzech połączonych segmentów linii. W przeciwieństwie do prostokąta lub kwadratu, w trójkącie kąty mogą mieć różne wymiary. Nie zawsze są to odpowiednie kąty. Trójkąty są nazywane w zależności od rodzaju kątów, które znajdują się w samym trójkącie. Na przykład, jeśli trójkąt ma jeden kąt prosty, będzie znany jako trójkąt prostokątny.

Jednak w przypadku, gdy wszystkie kąty trójkąta są mniejsze niż 90 stopni, zostanie on nazwany trójkątem ostrokątnym. Jeśli w ogóle, jeden z kątów w trójkącie mierzy więcej niż 90 stopni, będzie znany jako trójkąt rozwarty pod kątem. Wreszcie istnieje trójkąt równokątny, w którym wszystkie kąty trójkąta wynoszą 60 stopni. Z drugiej strony trójkąt można również zidentyfikować lub oznaczyć na typie boków, które mają.

Trójkąt łuskowaty nie ma przystających boków. Trójkąt równoramienny ma dwa przystające boki. Trójkąt równoboczny ma trzy przystające boki.

Należy pamiętać, że trójkąty równoboczne i równokątne to dwa odrębne terminy dla tego samego trójkąta.

Obwód

Najbardziej uniwersalnym wzorem na obliczenie obwodu trójkąta, możliwym do wykorzystania w przypadku każdego trójkąta jest wzór:

O = A + B + C

O — obwód koła

A, B, C — poszczególne boki trójkąta

Przykład

Obwód trójkąta o bokach A-3cm, B-3cm, C-3cm?

O = 3 +3 +3=9

Odpowiedź

Obwód trójkąta wynosi 9 cm.

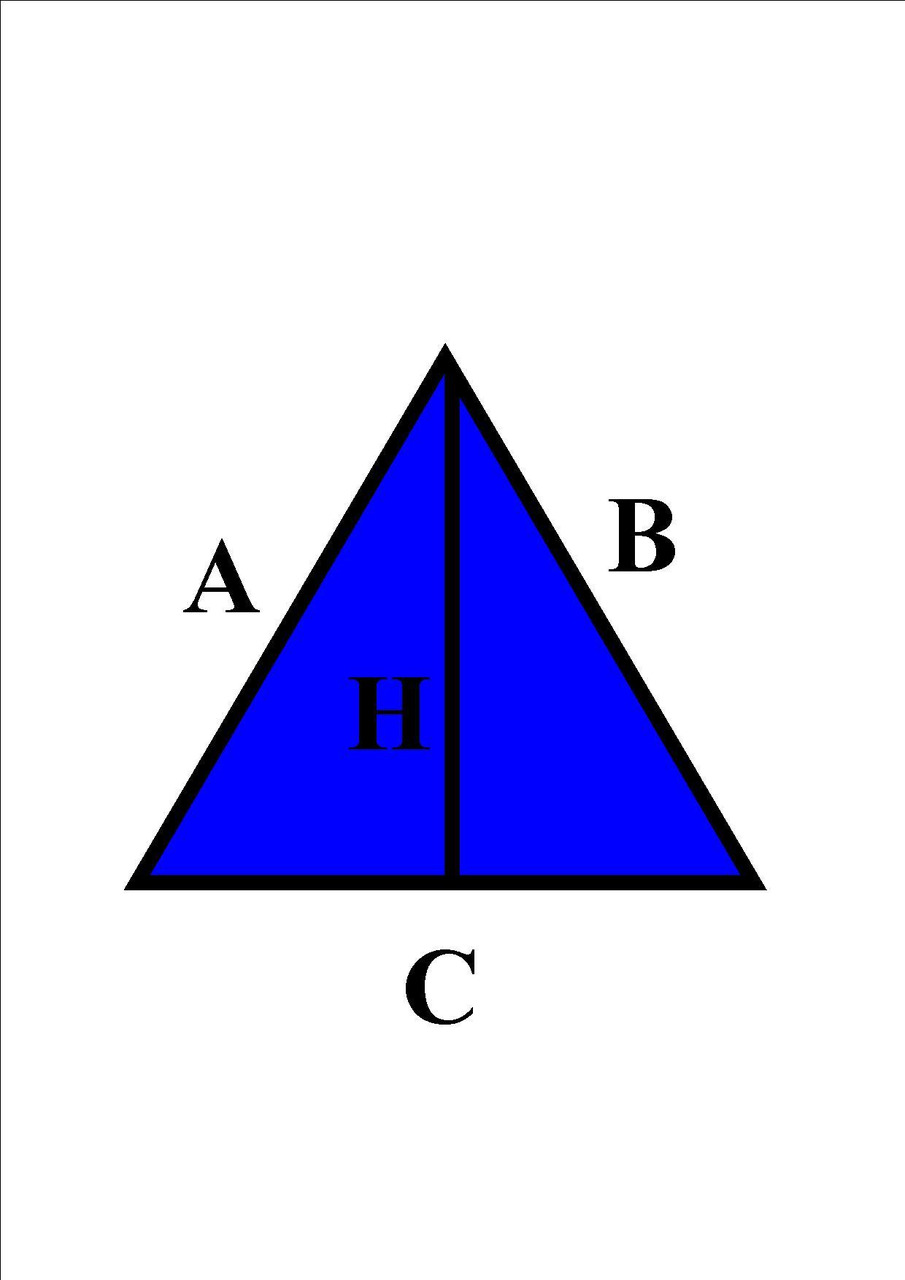
Pole

Pole trójkąta można obliczyć na wiele różnych sposobów. Wszystko zależy od tego jakimi danymi dysponujemy. Poniżej przedstawione zostały dwa podstawowe sposoby liczenia pola trójkąta.

Wzór 1

P=1/2*C*H

C — podstawa

H — wysokość

P — pole

Wzór 2

P= √(p(p-A)*(p-B)*(b-C))

A, B, C — poszczególne boki trójkąta

p- połowa obwodu trójkąta

p= (A+B+C)/2

Przykład

Przykład 1

Oblicz pole trójkąta o podstawie 6cm i wysokości 5,2cm

C=6cm, H=5,2cm.

P= 1/2*6*5,2=3*5,2= 15,6cm²

Przykład 2

Oblicz pole trójkąta o bokach 6cm,6cm, 6cm

A=6cm, B=6cm, C=6cm,

p= (6+6+6)/2=18/2=9cm

P= √(9*(9—6)*(9—6)*(9—6))

=√(9*(3*3*3))= √(9*27)= √243=15,588=15,6cm²

Odpowiedź

Pole trójkąta wynosi 15,6cm²

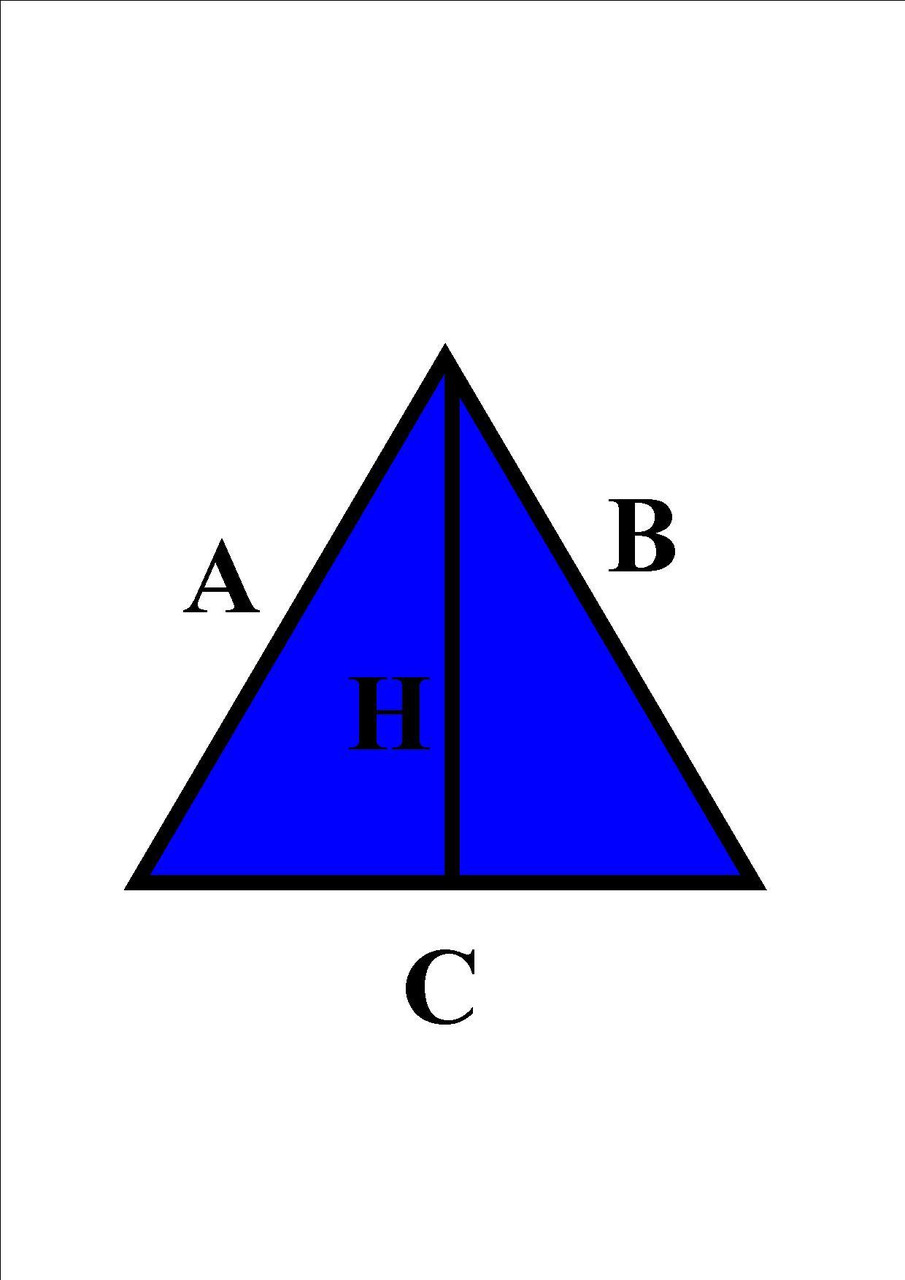
Wysokość

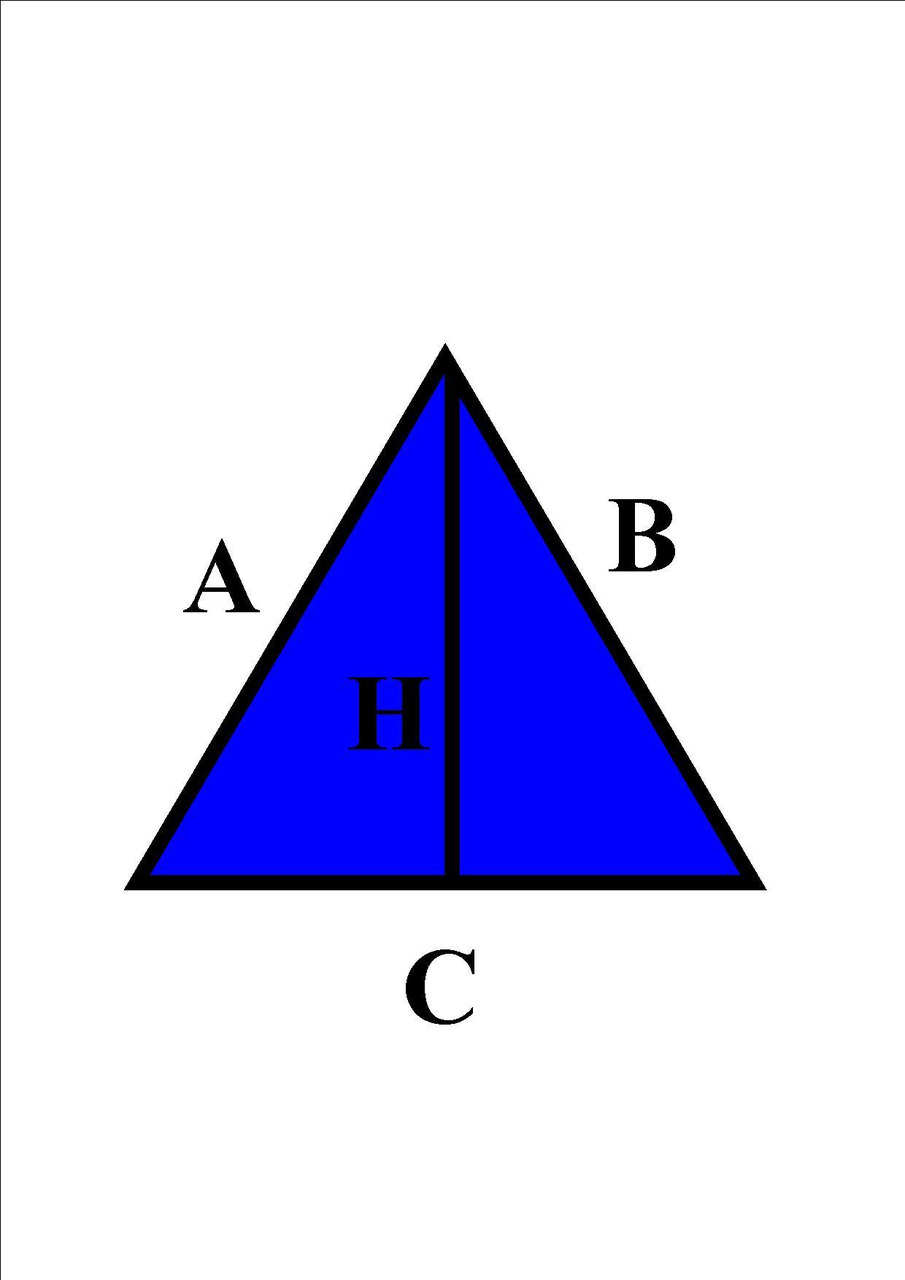
Wysokość trójkąta to najkrótszy odcinek łączący bok trójkąta z przeciwległym wierzchołkiem. To oznacza, że wysokość pada zawsze pod kątem prostym (w przeciwnym wypadku nie byłby to najkrótszy bok). Na matematyce wysokość trójkąta (oraz innych figur) oznaczamy literą H.

Wzór na wysokość trójkąta otrzymamy po przekształceniu wzoru na pole trójkąta czyli:

P=1/2*C*H

Po przekształceniu wzór na wysokość trójkąta wygląda następująco:

H= 2P/C

Przykład

Oblicz wysokość trójkąta o polu 15,6cm² i podstawie długości 6cm.

P=15,6cm²

C= 6cm

H= 2*15,6/6= 31,2/6=5,2cm

Odpowiedź

Wysokość trójkąta wynosi 5,2cm

Romb

Wstęp

Romb jest zamkniętą dwuwymiarową figurą płaszczyzny. Jest uważany za specjalny równoległobok, a ze względu na swoje unikalne właściwości uzyskuje indywidualną tożsamość jako czworokąt. Romb jest również nazywany czworokątem równobocznym, ponieważ wszystkie jego boki są równej długości. Termin „romb” pochodzi od starożytnego greckiego słowa „rhombos”, które w rzeczywistości oznacza coś, co się kręci.

Co to jest romb?

Romb można zdefiniować jako specjalny równoległobok, ponieważ spełnia wymagania równoległoboku, czyli czworoboku z dwiema parami równoległych boków. Oprócz tego romb ma wszystkie cztery boki równe tak jak kwadrat. Dlatego jest również znany jako pochylony kwadrat. poniżej został przedstawiony rysunek, aby zrozumieć związek kształtu rombu z równoległobokiem i kwadratem.

Obwód

Obwód rombu o boku a liczymy jako a*4

Przykład

Romb o boku a=5cm

Obwód liczymy 5cm*4=20cm

Odpowiedź

Obwód rombu wynosi 20cm