Bezpłatny fragment - Geometria obliczanie kątów w figurach zadania

Kąty wewnętrzne w trójkątach

Wstęp

Suma kątów wewnętrznych opisuje, jak duże są wszystkie kąty w figurze geometrycznej. Suma kątów wewnętrznych trójkąta jest zawsze równa 180°. Jest wiele różnych sposobów obliczania kątów wewnętrznych w trójkącie w zależności od tego jakimi danymi dysponujemy, poniżej zostaną przedstawione przykłady obliczania kątów w różnych trójkątach i posiadając różne informacje.

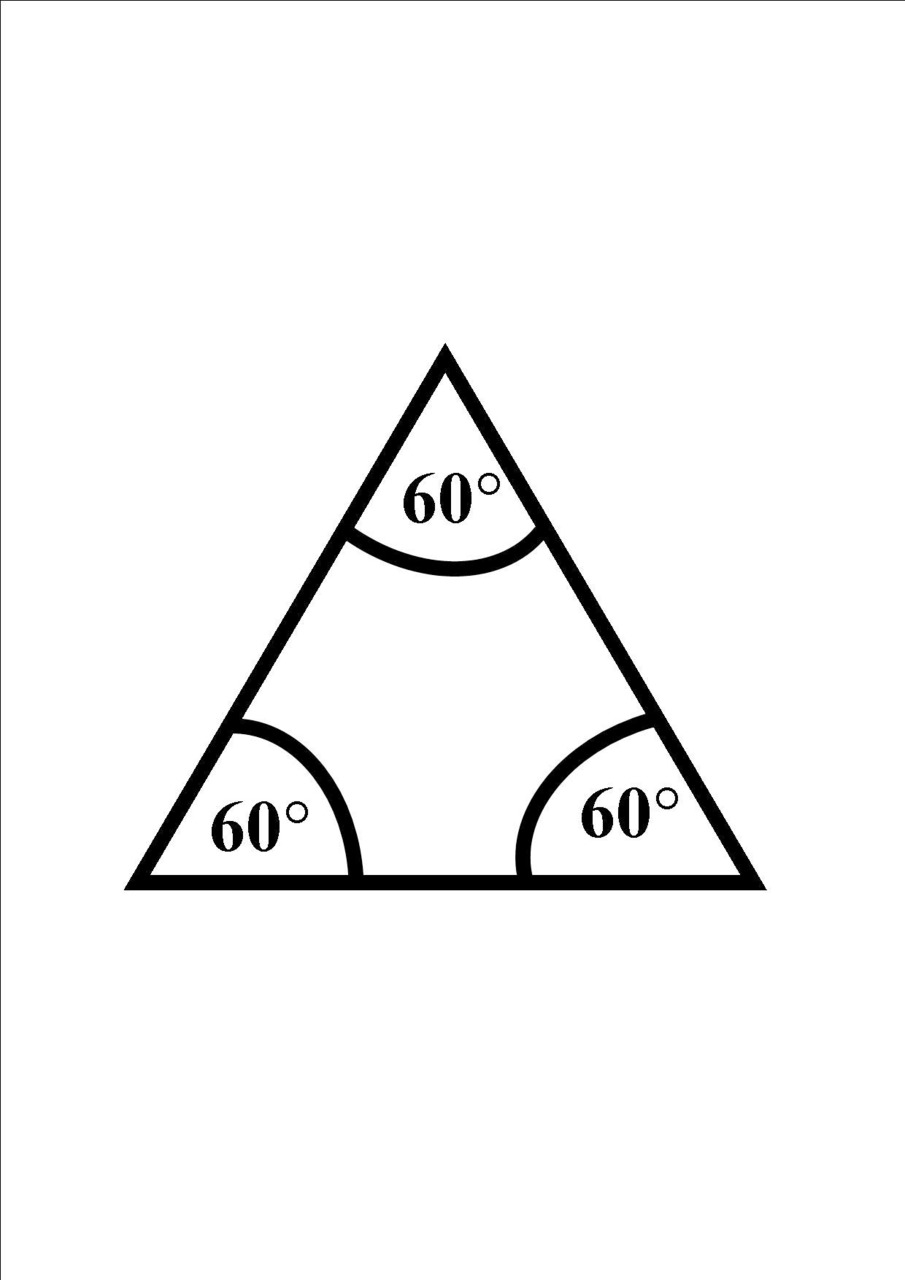
Przykład 1 trójkąt równoboczny

W trójkącie równobocznym każdy poszczególny kąt ma miarę 60° ponieważ wszystkie kąty są takie same.

Suma wewnętrznych kątów w trójkącie jest równa 180°.

Równanie

α= 180°/3= 60°

Odpowiedź

Kąty w trójkącie równobocznym mają następujące wartości:

α= 60°, β= 60°, γ= 60°

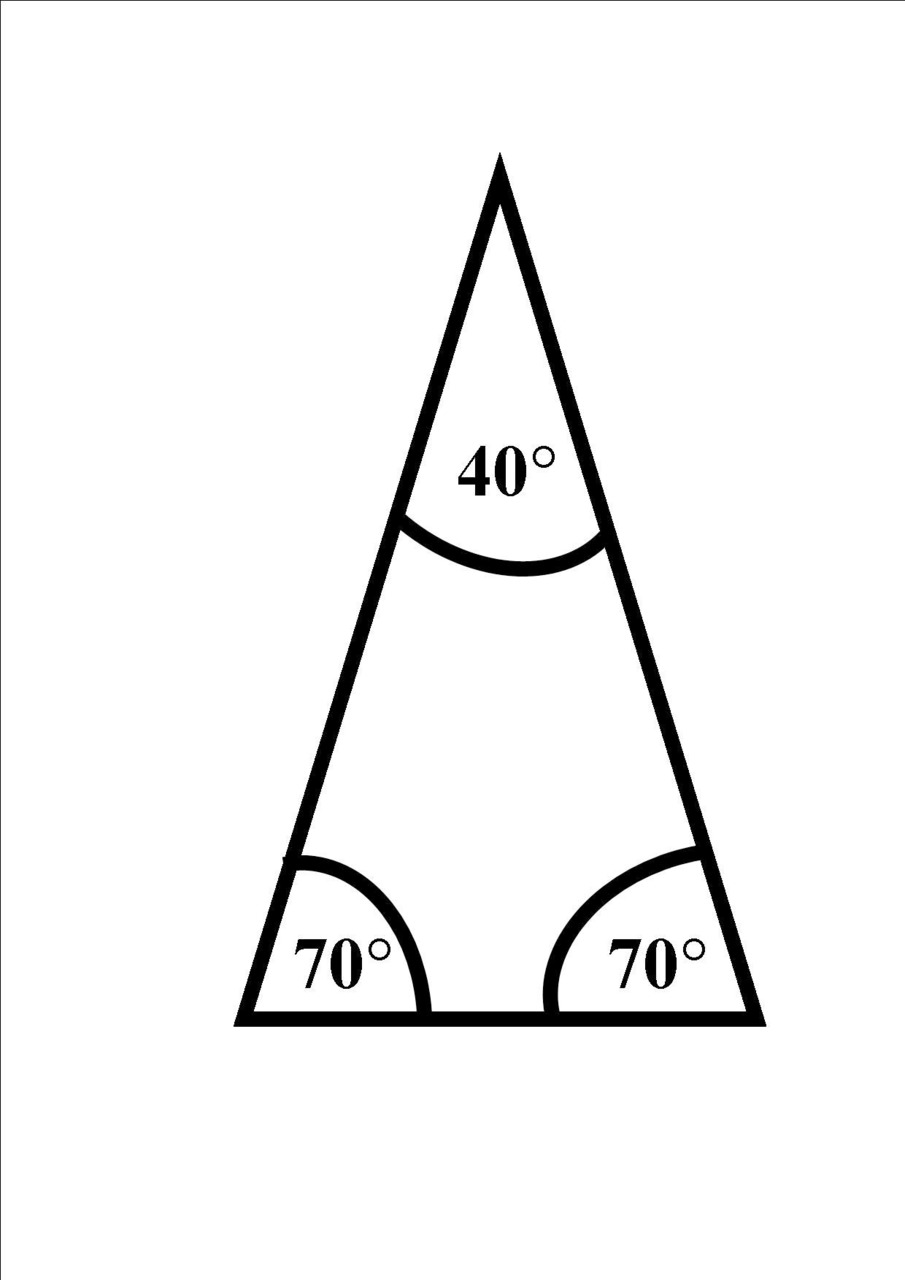
Przykład 2 trójkąt równoramienny część 1

W trójkącie równoramiennym dwa boki, jego ramiona mają tą samą długość, znaczy to, że 2 kąty w nim znajdujące się mają takie same wartości oraz to, że do obliczenia ich wystarczy wiedzieć ile wynosi kąt α.

Zadanie

W trójkącie równoramiennym kąt α= 40°, oblicz kąty w dwóch kątach znajdujących się przy ramionach tego trójkąta.

Rozwiązanie

α=40°, aby obliczyć pozostałe kąty β i γ należy zastosować wzór

(180°- α )/2= β i γ

β i γ= (180°- 40°)/2=140°/2= 70°

Odpowiedź

Pozostałe kąty β i γ mają wartość 70°.

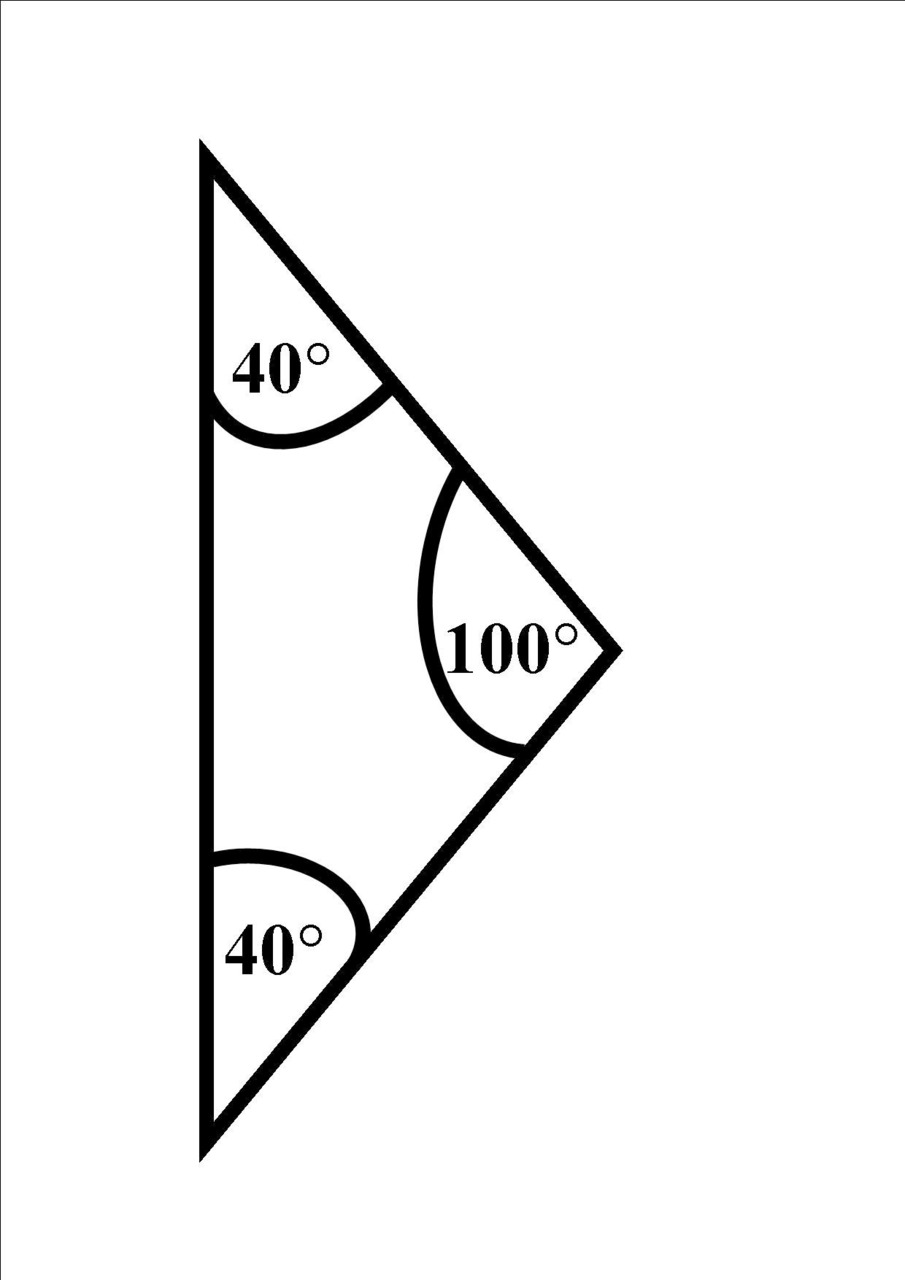
Przykład 3 trójkąt równoramienny część 2

W trójkącie równoramiennym dwa boki, jego ramiona mają tą samą długość, znaczy to, że 2 kąty w nim znajdujące się mają takie same wartości oraz to, że do obliczenia ich wystarczy wiedzieć jaką wartość wynosi jeden z kątów w podanym trójkącie. W poniższym zadaniu przedstawiony został szczególny przykład trójkąta równoramiennego będącym jednocześnie trójkątem rozwartokątnym, czyli jest to trójkąt, którego jeden kąt jest rozwarty. Kąt rozwarty ma miarę większą niż 90°.

Zadanie

W trójkącie równoramiennym kąt przy podstawie β= 40°, oblicz kąt α znajdujący się przy podstawie oraz kąt między ramionami γ.

Rozwiązanie

β =40°, aby obliczyć pozostałe kąty α i γ zastosujemy następujące wzory.

β= α,

β= 40°

α= 40°

γ= 180°- α- β= 180°- 40°- 40°= 100°

Odpowiedź

Kąty w trójkącie równoramiennym mają następujące wartości:

β= 40°, α= 40°, γ= 100°

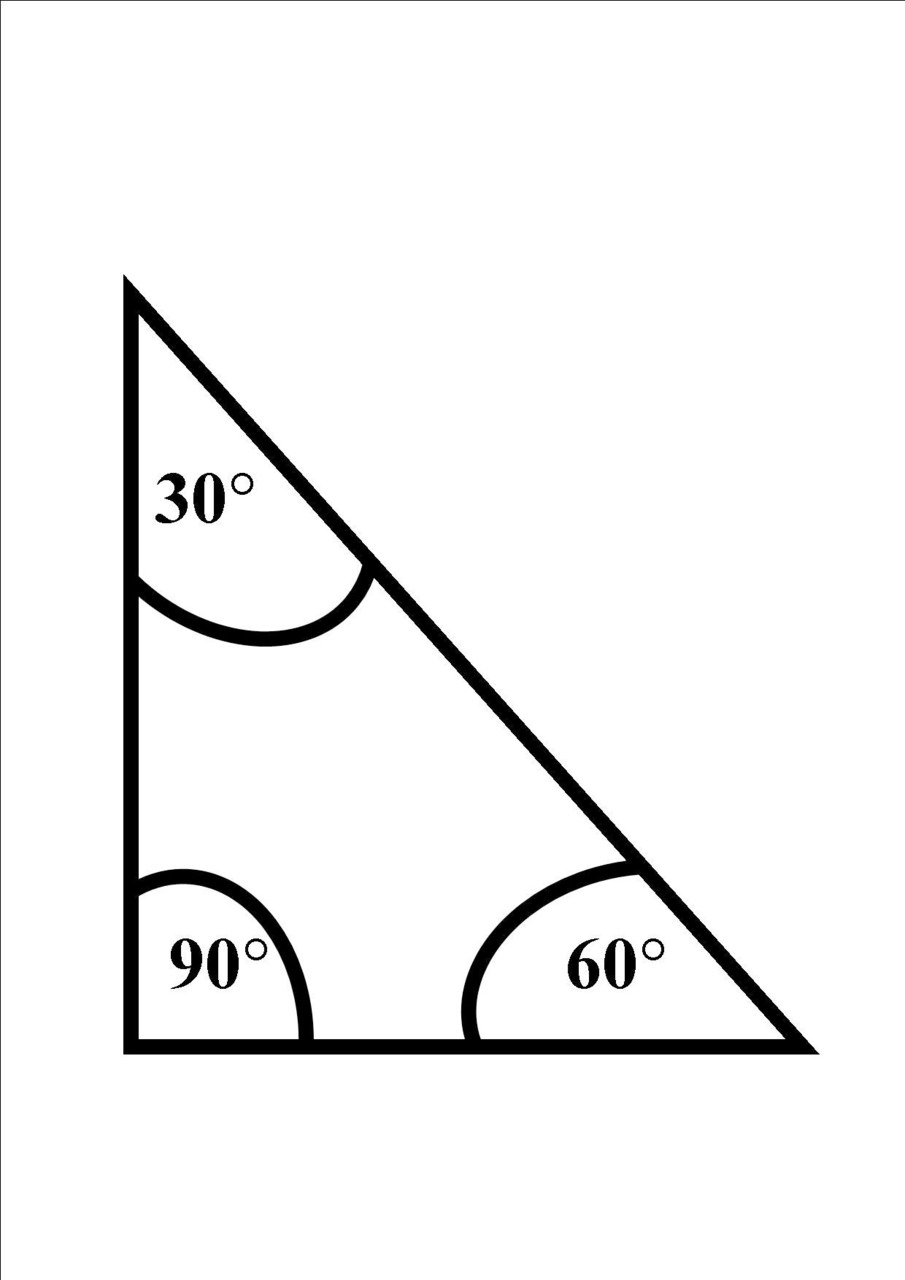
Przykład 4 trójkąt prostokątny część 1

W trójkącie prostokątnym jeden kąt zawsze jest równy 90° oraz dwa kąty ostre.

Zadanie

W trójkącie prostokątnym jeden z kątów ma wartość β= 30°, oblicz pozostałe kąty znajdujące się w tym trójkącie.

Rozwiązanie

α= 90°,

β= 30°,

aby obliczyć kąt γ należy zastosować wzór

γ= 180°-(α+β)

γ= 180°- (90°+30°)= 180°-120°= 60°

Odpowiedź

Kąty w trójkącie prostokątnym mają następujące wartości:

α= 90°, β= 30°, γ= 60°

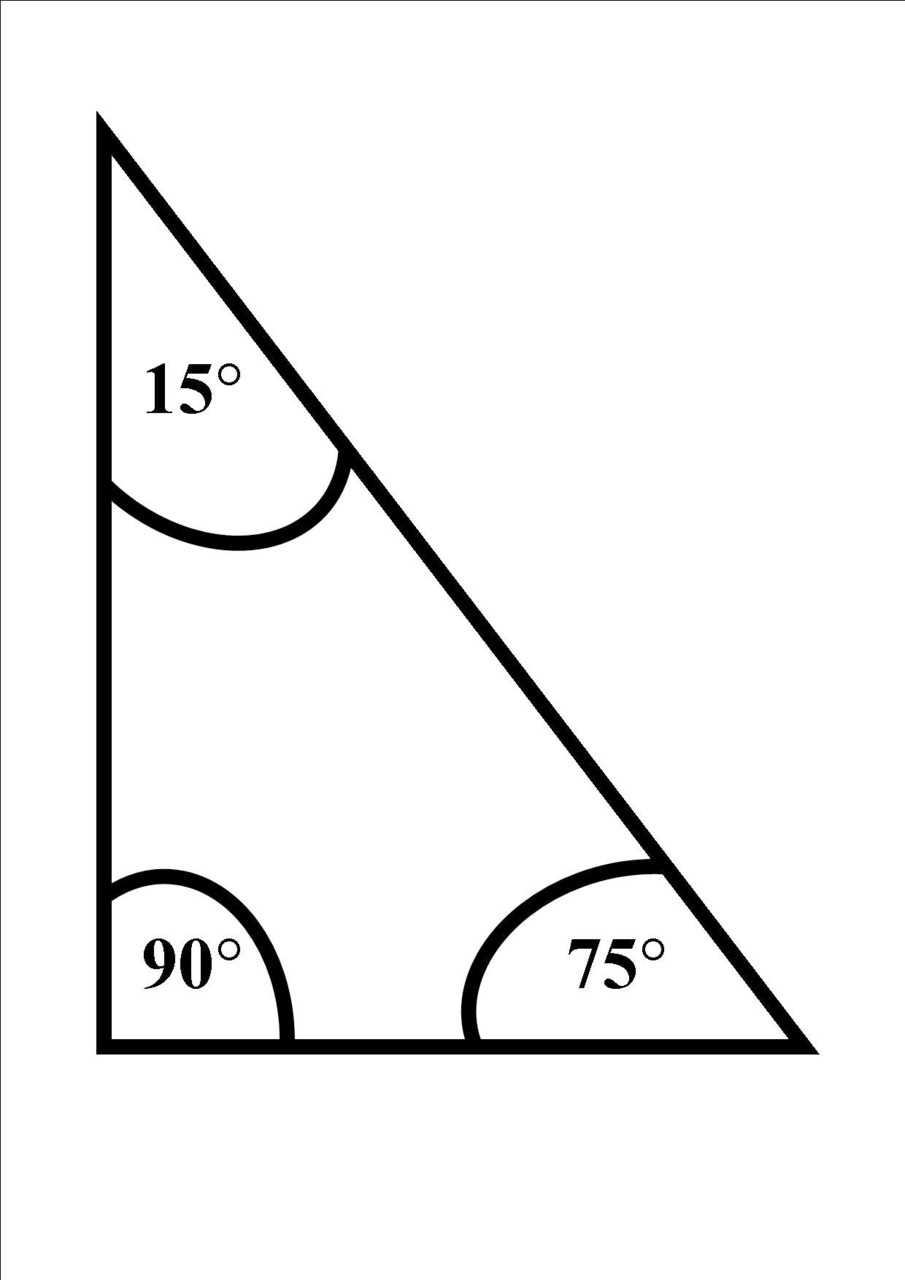
Przykład 5 trójkąt prostokątny część 2

W trójkącie prostokątnym jeden kąt zawsze jest równy 90° oraz dwa kąty ostre.

Zadanie

W trójkącie prostokątnym jeden z kątów ma wartość β= 75°, oblicz pozostałe kąty znajdujące się w tym trójkącie.

Rozwiązanie

α= 90°,

β= 75°,

aby obliczyć kąt γ należy zastosować wzór

γ= 180°-(α+β)

γ= 180°- (90°+75°)= 180°-165°= 15°

Odpowiedź

Kąty w trójkącie prostokątnym mają następujące wartości:

α= 90°, β= 75°, γ= 15°

Przykład 6 trójkąt prostokątny część 3